私と理論

数学の話を主に書きます

輸送問題と More-for-Less パラドックス

皆さん，パラドックスは好きですか？僕は大好きです．高校生の時の愛読書の一つがウイリアム・パウンドストーンの「パラドックス大全」だったくらいです．パラドックスが提示する思考の迷路をうろうろして途方に暮れるのはとっても楽しいですね．

最近，ネットワークフロー（輸送問題）における More-for-Less パラドックスを知ったので紹介します．

注意として，パラドックスは妥当そうな仮定から「論理的な矛盾」を導くもの（ラッセルのパラドックスなど）と「直感的でない結論」を導くもの（誕生日のパラドックス，バナッハ・タルスキのパラドックスなど）の二種類に大別することができますが，More-for-Less パラドックスは後者に分類されるものです．

輸送問題

輸送問題とは以下のような問題です．

  • n 件の工場と m 件の店舗からなる，ある商品の流通圏があるとする．
  • 各工場 i には a_i \geq 0 個の在庫がある.．
  • 各店舗 j では b_i \geq 0 個の需要がある．
  • 在庫の総和と需要の総和は等しいとする （すなわち \sum_{i \in [n] } a_i = \sum_{i \in [m]} b_i ）．
  • 工場 i から店舗 j に商品を一つ運ぶためには C_{ij} の輸送コストがかかる．
  • 各工場 i から各店舗 j への輸送量 x_{ij} を適切に決めて，各店舗の需要を満たしつつ輸送コストの総和を最小化せよ．

輸送問題は古くから研究されていながらも最新の機械学習界隈などでも盛んに取り組まれている，非常に重要な問題です．より詳しく知りたい方は以前僕が書いた 記事 などを参考にしてください．

More-for-Less パラドックス

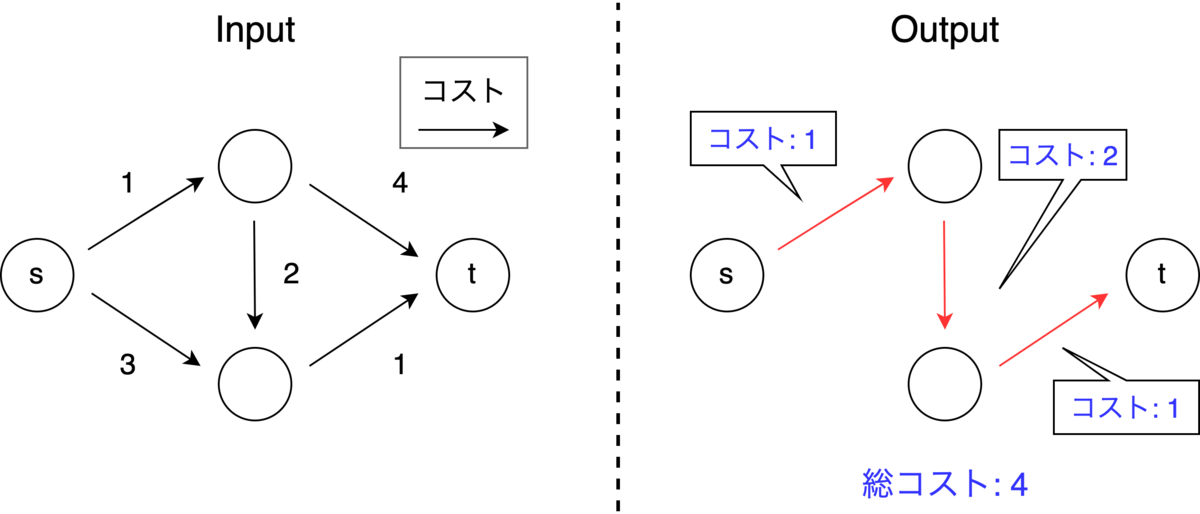
図 1 左 のような輸送問題を考えます ( n = 3, m = 4)．辺の横に書いてある値が輸送コストです．

f:id:Theory_and_Me:20210724142859p:plain
図1 考える輸送問題（左）と最適解（右）

この問題を解いてやると，最適解は図 1 右（辺の横に書いてあるのが輸送量）のようになり，必要コストは 152 となります．

さてここで，先ほどの例においてグラフの形状やコストは変化させず， a_2 の値を +2， b_4 の値を +2 した問題（図 2 左）を考えてみます．

f:id:Theory_and_Me:20210724143635p:plain
図2 変更した輸送問題（左）と最適解（右）

この問題は先ほどの問題と比較して 輸送する必要のある量が真に増加している ので，必要なコストは大きくなることが予想されます．いったいどの程度大きくなるのでしょう？

この問題における最適化は図 2 右のようになります．そして，必要コストは 150 になります．なんと，必要コストは増えるどころか減っているのです！

輸送しなければいけない量は増えているのに必要な（最小）コストは減ってしまう，これが輸送問題における More-for-Less パラドックスです．

なぜこんなことが起こるのか？

1つ目の問題の最適解から2つ目の問題の最適解への変化を見てみると，

  • 1→4（コスト 1）の輸送量が +2
  • 2→6（コスト 1）の輸送量が +2
  • 1→6（コスト 3）の輸送量が -2

となっています．つまり，輸送しなければいけない量（ \boldsymbol{a}, \boldsymbol{b}）が増えることによって，コストが小さい辺（1→4, 2→6）のみ使ってのやりくりが可能になるために，コストの大きい辺（1→6）を使う必要がなくなり，結果として総コストが減少しているのです．

こうして解をちゃんと観察すると「それはそう」な感じもしますが，依然として非直感的でもあります．直感に頼った推測は危険なことがわかりますね！

参考文献

このパラドックスの初出は [1] のようです（文献が見つからず読めていません）．問題例は [2] を参考にしました．

  • [1] A. Charnes, D. Klingman. The "More-for-Less" Paradox in the Distribution Model. Cahiers du Centre d'Études de Recherche Opérationnelle 13, 11-22, 1971.
  • [2] R. A. Ahuja, T. L. Magnatti, J. B. Orlin. Network Flows: Theory, Algorithms, and Applications. Princeton-Hall, 1993

輸送問題を近似的に行列計算で解く（機械学習への応用つき）

輸送問題と呼ばれる問題があります． この問題は，普通は線形計画法やフローのアルゴリズムを使って解かれます． この記事では，この輸送問題を近似的に行列計算で解くアルゴリズム（エントロピー正則化 + Sinkhorn-Knopp アルゴリズム）を紹介します．

輸送問題とは

輸送問題とは以下のような問題です．

  • n 件の工場と n 件の店舗からなる，ある商品の流通圏があるとする．
  • 各工場には a_i \geq 0 個の在庫がある.．
  • 各店舗では b_i \geq 0 個の需要がある．
  • 在庫の総和と需要の総和は等しいとする （すなわち \sum_{i \in [n] } a_i = \sum_{i \in [n]} b_i ）．
  • 工場 i から店舗 j に商品を一つ運ぶためには C_{ij} の輸送コストがかかる．
  • 各工場 i から各店舗 j への輸送量 x_{ij} を適切に決めて，各店舗の需要を満たしつつ輸送コストの総和を最小化せよ．

輸送問題は最適化の歴史の中でもかなり初期から考えられている問題です． 現実世界での応用が多く，さらに最大マッチングや最小重みマッチングを特殊ケースとして含む，重要な最適化問題です． (2023/11/13 註: 工場の数と店舗の数は違っていても以下と同様の議論が可能です．この記事では，説明の簡単のため工場の数と店舗の数が等しいとしています)

さて，この問題は数式で書くと以下のような最適化問題になります．

\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R_{\geq 0}^{n \times n}}}.& && \sum_{i, j \in [n]} C_{ij} \cdot x_{ij} \\ \mathrm{s.t.}& && \sum_{j \in [n]} x_{ij} = a_i \quad \forall i \in [n], \\ &&& \sum_{i \in [n]} x_{ij} = b_j \quad \forall j \in [n] \\ \end{aligned} \end{align*} \tag{1}


\boldsymbol{x} は整数値であるという制約を加えることもありますが，今回は連続値だとしましょう．

この問題は線形計画問題と呼ばれる問題クラスに入りますので，線形計画問題のアルゴリズム（単体法，内点法）を用いて解くことができます． さらに言えば，この問題はその中でもさらに特殊な，最小費用流問題という問題に帰着することができ，専用のアルゴリズムを適用することでより高速に解くことができます．

しかし，線形計画問題や最小費用流問題を解くためのアルゴリズムは比較的複雑で，実装するのは一手間です． また，計算量が \Theta (n^3) 程度かかるのであまりスケールしません． これらの問題を解決するアルゴリズムはないのでしょうか？

実は近似解で良ければそのようなアルゴリズムを構築することができます． このアルゴリズムは以下の特長を持ちます．

  • 実装が簡単
  • 速い
  • 単純な行列計算のみからなるので GPU などで高速化も可能

これが，本記事のテーマである「エントロピー正則化項を加えた輸送問題を Sinkhorn-Knopp アルゴリズムを用いて解く手法」です．

アルゴリズム

アルゴリズムは以下です．

  1. ハイパーパラメータ \lambda > 0 を決める．
  2. K_{ij} = \exp(-\lambda \cdot C_{ij}) で定義される行列 K を計算する．
  3. ベクトル \boldsymbol{u} \in \mathbb{R}^{n} を \boldsymbol{u} \leftarrow [1, 1, \ldots, 1] と初期化する．
  4. 「 \boldsymbol{v} \leftarrow \boldsymbol{b} \ / \ (K^{\top} \boldsymbol{u} ) の後に \boldsymbol{u} \leftarrow \boldsymbol{a} \ / \ (K \boldsymbol{v} )」 という計算を， \boldsymbol{u} が収束するまで繰り返す．ただし， / はベクトルの要素ごとの除算を意味する．
  5. U, V をそれぞれ \boldsymbol{u}, \boldsymbol{v} の要素を対角に並べた行列として，行列 UKV を出力する．

これだけです．とてもシンプルですね．20行くらいで実装できそうです．なんとこのシンプルなアルゴリズムがかなり良い解を出力してくれるのです．

ハイパーパラメータ \lambda > 0 は，アルゴリズムの性能をコントロールします． \lambda が大きいほど出力が真の解に近づきますが，収束が遅くなります．また， K_{ij} = \exp(-\lambda \cdot C_{ij}) を計算する必要があるため， \lambda が大きいとき数値的に扱いが難しくなります．

得られる解の例

ランダムに作った輸送問題のケースを，最小費用流及び Sinkhorn-Knopp アルゴリズムで解いた際の解 \boldsymbol{x} の様子を図示したのが以下の図です． 左上が最小費用流のアルゴリズムによる最適解であり，それ以外は \lambda を色々変えた場合の Sinkhorn-Knopp アルゴリズムの出力です．

解 x の例．SK は Sinkhorn-Knopp の略

見ての通り， \lambda を小さく設定した場合は Sinkhorn-Knopp アルゴリズムの出力は「ボヤッと」していて最適解からは程遠いですが， \lambda が大きくなるにつれて最適解に近づいていることが分かります．それに伴い，目的関数値も最適値に近づいていきます．ちなみに全ての \lambda について，制約を（ほぼ）満たす解が出力されています．

なぜこれで解けるのか？

気になるのはなぜこんなアルゴリズムで輸送問題が解けてしまうか？です．これについて，数学的に厳密な議論ではないですが直感的に説明します．

実は，このアルゴリズムは輸送問題を少し変形した以下の問題を解いています．


\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R_{\geq 0}^{n \times n}}}.& && \sum_{i, j \in [n]} C_{ij} \cdot x_{ij} \color{red}{+\frac{1}{\lambda} \sum_{i, j \in [n]} x_{ij} \log x_{ij}} \\ \mathrm{s.t.}& && \sum_{j \in [n]} x_{ij} = a_i \quad \forall i \in [n], \\ &&& \sum_{i \in [n]} x_{ij} = b_j \quad \forall j \in [n] \\ \end{aligned} \end{align*} \tag{2}


目的関数に何か余計な項が入っていますね． \sum_{i, j \in [n] } x_{ij} \log x_{ij} という項は， \boldsymbol{x} を確率分布と見做した場合のシャノンのエントロピー（に -1 をかけたもの）として捉えることができます．そのため，この項はエントロピー正則化項と呼ばれます．

\lambda は エントロピー正則化の強さをコントロールする係数です． \lambda が大きくなるともとの輸送問題に近づき，小さくなるともとの輸送問題から遠ざかります． エントロピー正則化項を小さくするということは， \boldsymbol{x} を全体的に「ボヤッとさせる」「曖昧にさせる」ことになります（ \boldsymbol{x} の要素が全て等しい場合にエントロピーは最大になる）．

さて，エントロピー正則化項を足した新しい最適化問題について，ラグランジュ関数を書いてみると，

\begin{align*} L(x, \boldsymbol{\alpha}, \boldsymbol{\beta}) = \sum_{i, j \in [n] } \left( \frac{1}{\lambda} x_{ij} \log x_{ij} + C_{ij} x_{ij} \right) + \boldsymbol{\alpha}^{\top} \left(x \boldsymbol{1}_{n} - \boldsymbol{a} \right) + \boldsymbol{\beta}^{\top} \left(x^{\top} \boldsymbol{1}_{n} - \boldsymbol{b} \right) \end{align*}


となります．ただし， \boldsymbol{1}_{n} は 全ての要素が 1 の n 次元縦ベクトル， x は x_{ij} を並べた n \times n 行列です．

このとき簡単な計算によって，全ての i, j \in [n] について

\begin{align*} \frac{\partial L}{\partial x_{ij}} = 0 \Rightarrow x_{ij} = u_i \cdot K_{ij} \cdot v_j \end{align*} \tag{3}


となります．ただし， u_i := e^{-\frac{1}{2} -\lambda \alpha_i}, v_j := e^{-\frac{1}{2} -\lambda \beta_j} とおきました．

数式 (3) の言っていることは，「行列 x は，行列 K の i 行目に u_i を， j 列目に v_j を掛けた形になっている」ということです．

さらに，行列 x はもとの問題の制約

\begin{align*} \sum_{j \in [n]} x_{ij} &= a_i \quad \forall i \in [n] \tag{4} \\ \sum_{i \in [n]} x_{ij} &= b_j \quad \forall j \in [n] \tag{5} \end{align*}


を満たす必要があります．

(3)(4)(5) を満たすような行列 x （もしくは \boldsymbol{u} 及び \boldsymbol{v}）を見つけるため，以下のような簡単なアルゴリズムを考えてみます．

  1. \boldsymbol{u} を適当に初期化する．
  2. \boldsymbol{u} を固定し，(4) の条件は一旦無視して，(3)(5) の条件を満たすようにうまく \boldsymbol{v} を決める．これは， \boldsymbol{v} \leftarrow \boldsymbol{b} \ / \ (K^{\top} \boldsymbol{u} ) とすれば OK．
  3. \boldsymbol{v} を固定し，(5) の条件は一旦無視して，(3)(4) の条件を満たすようにうまく \boldsymbol{u} を決める．これは， \boldsymbol{u} \leftarrow \boldsymbol{a} \ / \ (K \boldsymbol{v} ) とすれば OK．
  4. 2, 3 を収束するまで繰り返す．

行の定数倍と列の定数倍を，制約を満たすように交互に繰り返すイメージです． このアルゴリズムが，まさに Sinkhorn-Knopp アルゴリズムと呼ばれるものです． 直観的で単純なアルゴリズムですが，実はこのアルゴリズムがうまくいくことを理論的に示すことができます． 特に，

  • 問題 (2) にはユニークな最適解が存在すること
  • 上記のアルゴリズムの出力がユニークな最適解に収束すること

が示されています． 厳密な数学的な議論に関しては この論文 の Chapter 4 などを参照してください．

競プロの問題を解いてみる

紹介したアルゴリズムは近似解法であり，厳密な最適解を求めさせることの多い競プロの問題（特にマラソンではなくアルゴリズムのコンテスト）では適用は難しそうです． しかしどこまで解けるのかも気になるということで， opt さん (@opt_cp) がいくつかの問題（これとこれ）に挑戦してくれました！

方法は，輸送問題として定式化→エントロピー正則化 + Sinkhorn-Knopp アルゴリズムで解く→結果を適当に丸めることで整数実行可能解を得る，というものです．

結果としては，

  • ACを取るのは難しそう
  • ハイパーパラメータ \lambda の調整が難しい．小さいと最適解から離れてしまうし，大きいと収束が遅い＆オーバーフローする．オーバーフローの問題は logsumexp を用いたテクニック（詳細はこれを参照）で回避できるが，丸めて厳密解が得られるくらいの精度に辿り着くにはやはり反復回数が足りない．
  • ただ，それほど大きくないケースなら通せる．また，行列のサイズが 10000 \times 3 くらいなら（この記事ではコスト行列が正方行列の場合を扱ったが，そうでない場合にも簡単に一般化可能），最適値が 10^{13} くらい (整数) になる問題も 2sec 以内に厳密に解けることがあった．

という感じのようです．ただ，今回適用したのはかなりシンプルな手法であり，色々と発展手法もあるようなので，それらを用いればまた状況も変わるかもしれません．また，厳密解が必要ではない場面（マラソンなど）では使える可能性はあると思います．

機械学習界隈における流行

さて，話は変わるのですが，輸送問題を Sinkhorn-Knopp アルゴリズムで解く周辺の話は機械学習界隈で大流行しています．このことについて少し説明します．

冒頭の問題では \boldsymbol{a} や \boldsymbol{b} は商品の量として説明しましたが，これを n 次元空間における確率分布（確率ベクトル）として捉えてみましょう． 例えば \boldsymbol{a} = [0.3, 0.1, 0.6] などは 3 次元確率ベクトルです．

このとき，問題 (1) の最適値は，「確率分布 \boldsymbol{a} から確率分布 \boldsymbol{b} に確率を輸送する際に，必要な最小コスト」になります．これを L(\boldsymbol{a}, \boldsymbol{b}) と書くことにしましょう． 実は， L(\boldsymbol{a}, \boldsymbol{b}) は，確率分布 \boldsymbol{a} と確率分布 \boldsymbol{b} の近さ，つまり確率分布間の距離として用いることができます．実際，コスト行列 C_{ij} が距離の公理を満たすとき， L(\boldsymbol{a}, \boldsymbol{b}) も距離の公理を満たす距離関数になることが知られています． L(\boldsymbol{a}, \boldsymbol{b}) は最適輸送距離と呼ばれます．

さて，機械学習においては確率分布間の近さを測ることはひじょーーーーーーに重要です． 最も基本的な操作と言っても良いくらいだと思います． 一般にこの用途でよく用いられるのは Kullback-Leibler Divergence や Jensen–Shannon Divergence などの尺度です． しかし，最適輸送距離はこれらにはない特長をいくつも持つため，重要視されています（「もとの空間の距離を反映した確率分布間の距離になっている」「二つの確率分布のサポートが一致しない場合にも定義できる」など）．

このような重要な最適輸送距離ですが，一つ大きな欠点を抱えていました．計算量です．というのも，最適輸送距離を求めるためには上で述べたように輸送問題を解く必要があり，大きな計算量がかかってしまいます．機械学習ではかなり高次元の確率分布も扱うので，この計算量は重すぎます．

この問題を解決し，最適輸送距離の応用範囲を大きく広げたのが，今回紹介した Sinkhorn-Knopp アルゴリズムによる近似的な最適輸送距離の計算です． この手法は NIPS 2013 の "Sinkhorn Distances: Lightspeed Computation of Optimal Transport" という論文で提案されました． 現在ではこの論文は 1400 件近く引用されている，この分野では記念碑的な論文になっています． 流行は続いており，最適輸送に関する論文が機械学習の国際会議である NeurIPS や ICML，ICLR などでも現在でもたくさん発表されているという状況です． （ただ，最適輸送が流行っているのは，最適輸送を使った GAN が有名になった等の別の理由もあったりします）

ちなみに，この最適輸送問題は Monge-Kantorovich の問題と呼ばれたりもして，競プロでお馴染み Monge さんがこんなところにも現れます． また，コスト行列 C が Monge 性を満たす場合，輸送問題は効率的に解けるという話もあったりします．

まとめ

ややこしそうな最適化問題がこんな単純な行列計算で（近似的に）解けるのはけっこーびっくりですね． アルゴのコンテストでは厳しいかもだけどマラソンとかでは使えることがあるかもね

公開前にこの記事を読んで有益なコメントをたくさん下さった opt さん (@opt_cp) に感謝します．

ネットワークフロー問題たちの関係を俯瞰する

ネットワークフロー好き好きマンとして，フローを布教したくなったので記事を書きました． ただし，フローの解説資料は既に素晴らしいものがたくさんあるので，今回は今まであまり焦点が当てられてこなかった部分を推して話をしたいと思います．

テーマは，数あるフローの問題の関係を整理することです． フローの問題たちには共通の歴史があり，共通の定式化があり，共通のアルゴリズムの思想があります． その「共通」の部分を理解することで，フローに対する理解が深まり，より面白いと感じられると僕は思っていて，そこについて書きます．

かなり基本的な内容しか書いてないので，強い人が得るものはあまりないかもしれません． あとこの記事はおきもちを書いてる部分が多いです．

また，この記事では問題の話だけをしてアルゴリズムの詳細の話をほとんどしません．この辺りは 保坂さんのスライド などが非常に分かりやすいので，そちらを参照してもらうと良いと思います．

そもそもネットワークフロー問題ってなんなんだ

簡単に言うと，「グラフ上で」「各辺に流体のようなものを流すときに」「各頂点における（流出量）−（流入量）に関する制約のもとで」「何らかの目的関数を最適化する」問題である，と言うことができます．

数学的に書くと以下のようになります．

  • 有向グラフ G=(V, E) が与えられる．
  • 各辺 (i, j) \in E に「流体のようなもの」を流すことを考える．各辺の流量 x_{ij} からなるベクトル x = [x_{ij} \mid (i, j) \in E] をフローと呼ぶ．
  • フローは，各頂点 i \in Vにおいて，実数 b_i によって指定される供給・需要制約を満たす必要がある．数学的に書くと， i \in V について \partial x_i := \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} x_{ji} と定義したとき， \partial x_i = b_i が成り立つ必要がある．
  • 何らかの目的関数を最適化するようなフローを求める．

本質的に重要なのは供給・需要制約です． \partial x_i の定義の第一項は「頂点 i から流出するフロー量」を，第二項は「頂点 i に流入するフロー量」を表しているので，

  • b_i = 0 ならば流量保存則が成立している必要がある．
  • b_i > 0 ならば流出が流入より大きい必要がある．このような頂点は供給点と呼ばれる．
  • b_i \lt 0 ならば流入が流出より大きい必要がある．このような頂点は需要点と呼ばれる．

となります．

おきもちですが，ネットワークフロー問題の綺麗な構造は，供給・需要制約の性質の良さから来ているものだというイメージがあります．

他には辺ごとに「流せるフローの範囲の制約」がついてたりする場合もあります．

分野の概観

以下の図がフロー分野の概観になっています．ここに書かれているもの以外にもフローの問題はたくさんありますが，基本的なものはこの三つだと思います．

f:id:Theory_and_Me:20210401235911p:plain:w400
ネットーワークフロー分野の概観

この図の中で注目すべきポイントは以下です．

  1. 最短路問題 がフローに含まれています．最短路問題はフローとして説明されることは少ないですが，最短路がフローであることを意識すると分野の見通しが良くなります．

  2. 最小費用流問題は最短路問題と最大流問題の共通の一般化になっています．逆に言うと最短路問題も最大流問題も最小費用流問題の特殊ケースになっています．

1 について，最短路をフローとして捉えるのはフロー業界（？）ではかなり一般的です．フローer の聖書であるところの Ahuja, Magnanti and Orlin の "Network Flows: Theory, Algorithms, and Applications" (以下 Ahuja 本) も最短路問題→最大流問題→最小費用流問題を順に扱う，という流れになっています．

2 について，逆に言うと，最短路問題は「最小コスト」要素を，最大流問題は「容量」要素をそれぞれ最小費用流問題から切り出したものであると捉えることできます． これも僕が勝手に思っているだけの話ではなく， Ahuja 本にも同様の記述があります．

このような理解は解法を理解する際にも役に立ちます．後述しますが，最小費用流の最も基本的なアルゴリズムである最短路反復法は，「最小コスト」部分を最短路問題の方法論によって，「容量」部分を最大流問題の方法論によって解決したものであると解釈することができます．

ネットワークフロー問題たち

最短路問題

みなさんよく知っている，最適化問題の代表のようなやつです．わざわざ説明しなくてもいいかも知れませんが，一応問題を示しておきます．

  • 入力
    • 有向グラフ G=(V, E)
    • 各辺 (i, j) \in E のコスト c_{ij} \geq 0
    • スタートの頂点 s
    • ゴールの頂点 t
  • 出力:
    • G における s から t へのパスで，パス中の辺の重みの和が最小になるもの

f:id:Theory_and_Me:20210405195735p:plain
最短路問題

さて，最短路問題はネットワークフローの問題として捉えられます． というのも，各辺のコストを「その辺にフローを 1 流すのに必要なコスト」とすると，最短路問題は「 s から t へフローを 1 流す方法で，コストを最小にするものを求める問題」になるからです．（実はこれはコストが負の辺が含まれると怪しくて，これについては後述します）

最大流問題

ネットワークフローといえばこれを思い浮かべる人も多いんじゃないでしょうか？

以下のような問題です．

  • 入力
    • 有向グラフ G=(V, E)
    • 各辺 (i, j) \in E の容量 u_{ij} \geq 0
    • スタートの頂点 s
    • ゴールの頂点 t
  • 出力:
    • G における許容フローで，総流量が最大になるもの

ただし「許容フロー」と「総流量」は以下のように定義されます．

  • 許容フローとは，以下の二つの条件を満たすフローである:

    • 全ての i \in V \setminus \{s, t \} に対して \partial x_i = 0 が成り立つ．
    • 全ての (i, j) \in E について 0 \leq x_{ij} \leq u_{ij} が成り立つ．

  • 総流量とは， \partial x_s = -\partial x_t のことである．

f:id:Theory_and_Me:20210405200052p:plain
最大流問題

簡単にいうと，「ネットワーク上で， s から t にできるだけ多くのものを運ぶ方法を求める問題」です．

最大流問題が特に重要視されるのは，問題自体の重要性も勿論ですが，二部グラフの最大マッチング，最小カット問題，（いわゆる）燃やす埋める問題など，重要な問題が最大流問題に帰着できるという要因も大きいと思われます．

最小費用流問題

知名度は最大流問題に劣る気もしますが（？），フロー界では非常に重要な最適化問題です．Ahuja 本にも "The minimum cost flow model is the most fundamental of all network flow problems. " という記述があるくらいです． 最大流問題は「できるだけ多く運ぶ」問題でしたが，最小費用流問題は「決まった量のものを」「できるだけ小さいコストで運ぶ」問題です． 最小費用流問題には定式化の仕方が色々あるのですが，代表的なものを二つ紹介します．

s-t フロー

s から t に総流量 B だけ流すという定式化です．

  • 入力
    • 有向グラフ G=(V, E)
    • 各辺 (i, j) \in E のコスト c_{ij} \geq 0
    • 各辺 (i, j) \in E の容量 u_{ij} \geq 0
    • スタートの頂点 s
    • ゴールの頂点 t
    • 総流量 B
  • 出力:
    • G における許容フローで，総コストが最小になるもの

ただし，許容フローとは，以下の二つの条件を満たすフローです:

  • i \in V \setminus \{s, t \} に対して \partial x_i = 0 ， \partial x_s = B ， \partial x_t = -B が成り立つ．
  • 全ての (i, j) \in E について 0 \leq x_{ij} \leq u_{ij} が成り立つ．

f:id:Theory_and_Me:20210414211320p:plain
s-t フロー

b-フロー

s や t といった特別な頂点を考えずに，各頂点の需要・供給量が与えられるとする定式化です．

  • 入力
    • 有向グラフ G=(V, E)
    • 各辺 (i, j) \in E のコスト c_{ij} \geq 0
    • 各辺 (i, j) \in E の容量 u_{ij} \geq 0
    • 各頂点 i \in V における需要・供給値 b_i．ただし， \sum_{i \in V} b_i = 0 が成り立つものとする．
  • 出力:
    • G における b-フローで，総コストが最小になるもの．

ただし，b-フローとは，以下の二つの条件を満たすフローです:

  • i \in V に対して \partial x_i = b_i が成り立つ．
  • 全ての (i, j) \in E について 0 \leq x_{ij} \leq u_{ij} が成り立つ．

f:id:Theory_and_Me:20210405200307p:plain
b-フロー

b-フローは競プロ方言だとなぜか思いこんでいたのですが，Korte and Vygen の「組合せ最適化」などでも使われている一般的な用語のようです．

二つの定式化の関係

s-t フローと b-フローはほとんど同じ定式化で，片方をもう片方に簡単に変形することができます． これを確かめてみましょう．

  • (s-t フロー → b-フロー) こちらは簡単で，単に b_s = B ， b_t = -B ， i \in V \setminus \{s, t \} に対して b_i = 0 としてやれば OK です．

  • (b-フロー → s-t フロー)

    • 頂点 s, t を追加する
    • b_i > 0 なる頂点 i について， s から i に向けてコスト 0，容量 b_i の辺を引く
    • b_i \lt 0 なる頂点 i について， i から t に向けてコスト 0，容量 b_i の辺を引く

の手順で OK です．

f:id:Theory_and_Me:20210412215449p:plain
b-フローから s-t フローへの変形

どちらの定式化が良いのか

個人的には b-フローで考える方が良いと思っています．理由は以下です．

  • 負コストの辺の除去が簡単にできる （snuke さんの記事）
  • 容量スケーリング法などの解法を用いる場合，アルゴリズム中で s-t フローではない形に問題をあえて変形することがあるため，最初から b-フローで考えた方が見通しが良い．（最も基本的な解法である最短路反復法では，s-t フローの形しか途中経過に出てこないのであまり気にならないけど）
  • LP (線形計画問題) としての定式化がとても綺麗に書けるので，双対を取るなどの LP を通した操作も見通しよく行える．

最大流問題は s-t フローの形であることが本質的でしたが，最小費用流問題では全く本質的ではなく，寧ろ b-フローの方が自然である印象です． misawa さんのライブラリ記事 でも b-フローの形が採用されていますし，上述の snuke さんの記事でも b-フローとして解釈することが推奨されています．Korte and Vygen の「組合せ最適化」や Ahuja 本でも b-フローで説明されていますね．

ただし，s-t フローにも，最大流との類似性から初心者がとっつきやすいという学習面での良さはあると思うので，初めはこちらで理解するのも良いと思います．

ネットワークフロー問題たちの関係

最短路問題は最小費用流問題の特殊ケース

まず，先に述べたように最短路問題は最小費用流問題の特殊ケースです．以下でこれを確認します．

最短路問題から，以下の手順で b-フローの問題を作ります．

  • 最短路問題におけるコスト c の辺を，（コスト c ，容量 1）の辺に置き換える
  • b_s = 1 ， b_t = -1 とし， i \in V \setminus \{s, t \} に対して b_i = 0 とする

作られた b-フローの問題を解くことでもとの最短路問題を解くことができます．

f:id:Theory_and_Me:20210412220138p:plain
最短路問題→最小費用流問題

ただし，もとの最短路問題に負の辺がある場合，特に負閉路がある場合は注意が必要です．以下のように，もとの最短路問題と最小費用流問題で最適値が異なる場合を作ることができてしまいます．

f:id:Theory_and_Me:20210412221309p:plain
最適値が異なる場合

このため，「負閉路が存在しない最短路問題は最小費用流問題の特殊ケース」と言った方が安全かもしれません． 一般的に，負閉路がある場合の最短路問題や最小費用流問題は取扱いに注意が必要な場合が多いです．

ちなみに負閉路が存在する場合に単純な最短路（同じ頂点を二度以上通らないパスの中で最短のもの）を求める問題は一般には NP-Hard です（これが多項式時間で解けるとハミルトン路の存在を多項式時間で判定できてしまう）．

最大流問題は最小費用流問題の特殊ケース

次に，最大流問題も最小費用流問題の特殊ケースであることを確認してみます．

最大流問題から，以下の手順で b-フローの問題を作ります．

  • 最大流問題における容量 u の辺を，（コスト 0 ，容量 u）の辺に置き換える
  • 頂点 t から 頂点 s に，（コスト -1 ，容量 +\infty）の辺を張る
  • i \in V に対して b_i = 0 とする

作られた b-フローの問題を解くことでもとの最短路問題を解くことができます．ただし最適解は符号が逆になっていることに注意して下さい．

ちなみに，このように全ての i \in V に対して b_i = 0 である最小費用流問題は最小費用循環流問題とも呼ばれます．

f:id:Theory_and_Me:20210412220218p:plain
最大流問題→最小費用流問題

おきもちとして，最短路問題→最小費用流問題はかなり直感的な変形ですが，最大流問題→最小費用流問題は少しトリッキーな変形です． こういう部分にも現れているのですが，個人的には最小費用流問題は，最大流問題の一般化と捉えるよりも最短路問題の一般化として捉えるのが理解しやすいのではないかと思っています．

最短路反復法のおきもち

最短路反復法は，最小費用流問題を解くためのアルゴリズムの代表的なものです． アルゴリズム自体の説明は省略しますので 保坂さんのスライド などを参照して下さい．

最小費用流問題が最短路問題と最大流問題の共通の一般化であることを意識すると，最短路反復法がとても自然な解法に見えるという話をします．

最小費用流問題の難しい点は，

「コストは最小にする」「容量制約も守る」「両方」やらなくっちゃあならないってのが「最小費用流問題」のつらいところだな

f:id:Theory_and_Me:20210403083035j:plain
ジョジョの奇妙な冒険 53巻より

です．最短路問題で扱う課題と最大流問題で扱う課題を同時に倒す必要があるのです．

そこで，最短路反復法は，この二つの課題を今までの問題で用いた道具を用いて解決します． つまり，「コストを最小にする」部分を最短路を用いることによって，「容量制約は守る」部分を最大流問題を解く際に用いる残余グラフのアイデアで倒します．

具体的には，「コスト付きの残余グラフ上でひたすら供給点から需要点への最短路を求めてそれに沿ってフローを流す」ということをします． 残余グラフ上のパスに沿ってフローを流すため容量制約は守られ，最短路にひたすら流すのでコストもなんとなく小さくなりそうな気がしてきます． これが最短路反復法です． 最小費用流問題が最短路問題と最大流問題の共通の一般化であることを意識すれば，最短路反復法はアルゴリズムとしてとても素直なものに見えてくるのではないでしょうか．

最短路反復は，現状での最短路を探してそこに流すのを繰り返すのでかなり単純な貪欲法だと捉えることができます．そんな雑な貪欲法でいいのかという気持ちになりますが，なんとこの出力は必ず最適解になることが証明できてしまいます！これはかなりびっくりするところで，最小費用流問題の綺麗な構造が現れている点でもあります．

実は，ネットワークフロー問題というのは妙に貪欲法がうまくいく問題群です．最短路反復法もそうですし，最大流問題に対するフォード・ファルカーソンのアルゴリズムもある意味貪欲法です．なぜ貪欲法がうまくいくのか，どんな問題で貪欲法がうまくいくのかという疑問は，離散凸解析という分野においてより抽象的な視点から分析されていたりします．

余談ですが，最短路反復法は1960年に伊理正夫という方（「数値計算の常識」という本でも有名ですね）が，他の海外の研究者と独立同時期に発見しました．また，「最短路反復法を行う時にポテンシャルを管理すると，辺のコストを全て非負にすることができるので，ダイクストラ法が使えて高速化できる」という初見では魔法のように見えるトリックは，1972年に冨澤信明という方が，これも他の海外の研究者と独立同時期に発見しました．この分野の発展は日本人の貢献に依るところも大きいようですね．

その他のネットワークフロー問題

今まで紹介した問題たちが代表的なネットワークフロー問題ですが，他にもネットワークフロー問題はたくさんあります．その一部を紹介します．この辺りは僕も理解していない部分も多いので，間違っていることを言っている可能性があります．何かありましたら教えて下さい．

  • 最小凸費用流問題． 最小費用流問題は単位流量あたりにかかるコストが枝に定義されていました．これは，各枝 (i, j) に流量 x_{ij} を引数とする線形のコスト関数 f_{ij}(x_{ij}) = c_{ij} \cdot x_{ij} が乗っていると考えることができます．このコスト関数を線形関数ではなく一般の凸関数にした問題を最小凸費用流問題といいます．最小凸費用流問題は，通常の最小費用流問題と似たような解法で効率的に解くことができます．AtCoder でも実は出題されたことがあります．詳しくは，Ahuja 本の14章を読むと良いです． 僕が一番好きなフローです

  • 一般化流問題． フローが各辺を通る間に増幅・減少するような問題設定も考えることができます．例えば，揮発性の液体を輸送するパイプネットワークにおいて，各パイプを通っている間に揮発によって一定割合で液体が減少してしまう，というような状況がこれに当てはまります．このような状況をモデリングしたのが一般化流問題です． 数学的には，各辺 (i, j) に増幅率 \mu_{ij} > 0 が定義されており，需要・供給制約が \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} \mu_{ji} \cdot x_{ji} = b_i に置き換えられます． 詳しくは，Ahuja 本の15章を読むと良いです．

  • 多品種流問題． ここまでのフローは一種類のフローを流す問題でしたが，一つのグラフ上で複数種類のフローを流す問題も考えられます．この問題を多品種流問題といいます．詳しくは Ahuja 本の17章にも乗っていますし，日本語の資料だと http://www.misojiro.t.u-tokyo.ac.jp/~hirai/papers/kouza.pdf などで解説されています．

  • パラメトリック最大流問題． 辺 (i, j) の容量が定数ではなく，パラメータ \lambda を用いて u_{ij}(\lambda) のような形で与えられている場合に，全ての \lambda に対して最大流問題を一気に解く問題です．特殊な条件下では効率的に解くことができるようです．英語ですが McCormick のスライド で解説されています．

他にも劣モジュラ流やらM凸劣モジュラ流やら動的流やら色々あるようです．また，そもそもグラフ構造を定義していない状態から，抽象的なパス（みたいな概念）から始めてフローの理論を構築するというようなことも行われているようです（例えば この論文 を参照して下さい）．気になる方は調べてみると良いと思います！

まとめ

フローは色々あって面白い！

公開前にこの記事を読んで有益なコメントを下さった Y.Y. さん (@ygussany) に感謝します．

imos 法を線形代数で理解・一般化して，フィボナッチ数列でも足せるようにする

この間の opt (@opt_coder) さん作の yukicoder の問題

No.1172 Add Recursive Sequence - yukicoder

において，imos 法を漸化式で表される数列の加算に一般化することが問われました． この一般化はパッと見何をしているか分かりにくいのですが，線形代数のレンズを通して見ることですっきり理解できると感じたのでこの記事にまとめます． この記事を読めば，通常の imos 法で想定される「ある区間の値に全て 1 を足す」クエリを超えて，「ある区間に 1, 2, 4, 8, \ldots を足す」「ある区間にフィボナッチ数列を足す」などのクエリが処理できるようになるはずです．

復習: imos 法

この記事では 1-indexed な記法を用います． imos 法は以下のような問題を解きたい時に用いる手法です．

  • 長さ N で値が全て 0 の配列 a に対して， Q 個の以下のクエリを適用する．
    • クエリ q : l_q \leq i \lt r_q なる各整数 i について， a_i に 1 を加算する

愚直に加算していこうとすると， \sum_{q=1}^Q ( r_q - l_q ) 回程度の加算が必要になるため， N や Q が大きいときに計算量が非常に多くなってしまいます．

この問題を解決するため，imos 法では以下のような計算を行います．

  • クエリ q について， a_{l_q} を +1 し， a_{r_q} を -1 する．
  • 最後に， i=1 から i=N-1 の順に a_{i+1} \leftarrow a_{i} + a_{i+1} という更新を行う．

こうすることで，正しい出力を 2Q + N 回程度の加算で計算することができます．典型 of 典型のようなテクニックなので使ったことがある人も多いと思います．

線形代数を通して imos 法を理解する

操作の理解

さて，この imos 法を線形代数の気持ちで理解していきます． そのために，配列を N 次元縦ベクトルで表現することにします． そして，ベクトル \boldsymbol{x}_q を l_q \leq i \lt r_q なる各整数 i について x_{q, i} = 1，それ以外の i については x_{q, i}=0 なるベクトルとして定義します（以降，このベクトルのことをクエリベクトルと呼びます）． このとき，計算したいものは \sum_{q=1}^Q \boldsymbol{x}_q になります．

さて，このような表記のもと，imos 法は実は以下のような操作をしていると理解することができます．

  • 正則行列 A に関して， \boldsymbol{y} := \sum_{q=1}^Q A \boldsymbol{x}_q を計算する．ただし， A は対角成分が 1 ， (i+1, i) 成分が -1 ，それ以外が 0 であるような行列．例えば， N=5 のとき
\begin{align} A = \begin{pmatrix} 1 & 0 & 0 & 0 & 0\\\ -1 & 1 & 0 & 0 & 0\\\ 0 & -1 & 1 & 0 & 0\\\ 0 & 0 & -1 & 1 & 0\\\ 0 & 0 & 0 & -1 & 1 \end{pmatrix} \\\ \end{align}

である．

  • A^{-1} \boldsymbol{y} を計算する．

ここで， A^{-1} \boldsymbol{y} = A^{-1} (\sum_{q=1}^Q A \boldsymbol{x}_q) = \sum_{q=1}^Q A^{-1} A \boldsymbol{x}_q = \sum_{q=1}^Q \boldsymbol{x}_q より，この操作が正しい解を出力することが保証されます．

気持ちとしては， 行列 A で表される線型写像によって一度全体を別の空間に飛ばし，そこでクエリを処理した上で A^{-1} によってもとの空間に戻す という感じです． ここで 写像が線形であることは本質的です : なぜなら A( \boldsymbol{x}+ \boldsymbol{y}) = A \boldsymbol{x} + A \boldsymbol{y} という線形性こそが飛ばした世界でクエリを処理することを正当化しているからです． また，写像が 正則 （逆行列が存在する）でないと情報が落ちてしまうのでもとの空間に戻せません．

具体例を見てみましょう． f:id:Theory_and_Me:20200823171222p:plain

黒の矢印が普通の計算手順を，赤の矢印が imos 法による計算手順を表します．

なぜ高速か？

これだけ見るとむしろ面倒で計算量が増えているだけに見えます． しかし，以下の 2 つの条件が満たされるため，この方法が非常に効率的になります．

(1) 全ての q=1, \ldots, Q について， A \boldsymbol{x}_q が スパース（非零要素数が少ない）である．

(2) A^{-1} \boldsymbol{y} が 高速に 計算できる．

この計算法に必要な計算の回数は， \mathrm{nnz}(\boldsymbol{x}) をベクトル \boldsymbol{x} の非零要素数， Iを A^{-1} \boldsymbol{y} の計算に必要な計算回数として \sum_{q=1}^Q \mathrm{nnz}(A \boldsymbol{x}_q) + I 程度となります． 従って，(1) (2) の条件が満たされる場合には非常に高速な計算法になり得るわけです．

(1) が成り立つことは，飛んでくるクエリベクトル \boldsymbol{x}_q において， x_{q, i} - x_{q, i-1} は高々 2 つの i を除いて 0 になることから確認できます．

f:id:Theory_and_Me:20200823171235p:plain

(2) が成り立つことを確認しましょう． A^{-1} \boldsymbol{y} を計算することは， A \boldsymbol{z} = \boldsymbol{y} なる連立方程式を \boldsymbol{z} について解くことに他なりません．この連立方程式は，

\begin{align} z_1 &= y_1, \\\ -z_1 + z_2 &= y_2, \\\ -z_2 + z_3 &= y_3, \\\ &\vdots \\\ -z_{N-1} + z_N &= y_N \\\ \end{align}

となりますが，これを変形すると

\begin{align} z_1 &= y_1, \\\ z_2 &= y_2 + z_1, \\\ z_3 &= y_3 + z_2, \\\ &\vdots \\\ z_N &= y_N + z_{N-1} \\\ \end{align}

となります．この式に従って z_1 から順番に計算していくと， z_i を計算する際には z_{i-1} は計算済みであるため， N 回程度の計算で \boldsymbol{z} が求められることがわかります．また，このようにして \boldsymbol{z} を求める手順は，通常の imos 法において最後に累積和を取っていく操作と同じであることも見てとれます．

一般化

さて，ここまでの議論を踏まえ，imos 法を一般化する方法を考えます．そのためには， なぜ imos 法がうまくいったのか を考えることが重要です．

  1. なぜ A \boldsymbol{x}_q がスパース になるのでしょう？　これは，飛んでくるクエリベクトル \boldsymbol{x}_q において，端である l_q, r_q 付近以外では x_{q, i} = x_{q, i-1} という線形の関係式が成り立つ からです．この性質から，適当な行列 A を取ってやることで l_q, r_q 付近以外では A \boldsymbol{x}_q を 0 にすることができるのです．

  2. なぜ A^{-1} \boldsymbol{y} が高速に計算できるのでしょう？　 これに関しては， A がスパースな下三角行列であることが重要です． A^{-1} \boldsymbol{y} を計算することは，線形方程式 A \boldsymbol{z} = \boldsymbol{y} を解くことに他なりません． このとき， A が下三角行列であれば， z_i に関する方程式に z_1, z_2, \ldots, z_{i-1} および y の要素しか出てきません． 従って z_1 から順番に求めていくことで， \mathrm{nnz}(A) 回程度の計算で \boldsymbol{z} を計算することができるのです． A がスパースであれば \mathrm{nnz}(A) は非常に小さくなり，高速な計算が実現できます． 一般の n \times n の係数行列を持つ線形方程式を普通に解こうとすると \Theta (n^3) 回程度の計算が必要であることから，これが非常に良い性質であることが見てとれます．

  3. A が下三角行列であることは， A の正則性の観点からも重要です．下三角行列に関する重要な事実として，行列式の値が対角成分の積に等しいというものがあります． A が正則 \Leftrightarrow A の行列式の値が非零 であることから， A は 対角成分が全て非零でありさえすれば正則 であることが保証されます．

逆に言えば，上記の性質が成り立つことを目指せば，別の問題においても類似の効率的な手法を設計することが可能です．これを見ていきましょう．

応用例

等比数列

次のような問題を考えてみましょう．

  • 長さ N で値が全て 0 の配列 a に対して， Q 個の以下のクエリを適用する．
    • クエリ q : l_q \leq i \lt r_q なる各整数 i について， a_i に 2^{i-l_q} を加算する

1, 2, 4, 8, \ldots というような数列を区間に足していくイメージです． ここでは簡単のため公比 2 の等比数列を考えていますが，他の公比の場合も同様の議論が可能です．

この問題を imos 法と同様にして処理することを考えましょう． 重要な性質は，各クエリベクトルにおいて 端である l_q, r_q 付近以外では x_{q, i} = 2 x_{q, i-1} という線形の関係式が成り立つ ことです． このことを考慮すれば， A \boldsymbol{x}_q をスパースにするためには， A として対角成分が 1 ， (i+1, i) 成分が -2 ，それ以外が 0 であるようなものを取れば良さそうです． 例えば N=5 のときは

\begin{align} A = \begin{pmatrix} 1 & 0 & 0 & 0 & 0\\\ -2 & 1 & 0 & 0 & 0\\\ 0 & -2 & 1 & 0 & 0\\\ 0 & 0 & -2 & 1 & 0\\\ 0 & 0 & 0 & -2 & 1 \end{pmatrix} \\\ \end{align}

です．この行列はスパースな下三角行列であり，さらに対角成分が全て非零であることから，必要な性質を全て備えています．

A^{-1} \boldsymbol{y} の計算，すなわち A \boldsymbol{z} = \boldsymbol{y} なる \boldsymbol{z} を求める操作は，

\begin{align} z_1 &= y_1, \\\ - 2 z_1 + z_2 &= y_2, \\\ - 2 z_2 + z_3 &= y_3, \\\ &\vdots \\\ \\ -2 z_{N-1} + z_N &= y_N \\\ \end{align}

より

\begin{align} z_1 &= y_1, \\\ z_2 &= y_2 + 2 z_1, \\\ z_3 &= y_3 + 2 z_2, \\\ &\vdots \\\ z_N &= y_N + 2 z_{N-1} \\\ \end{align}

となります．毎回値を 2 倍しながら累積和を取るイメージですね．

具体例で見てみましょう． f:id:Theory_and_Me:20200823171245p:plain

うまくクエリベクトルをスパースにしつつ正しい解を出力できていることが分かると思います．

フィボナッチ数列

更なる応用として，区間へのフィボナッチ数列の加算を考えてみましょう．

  • 長さ N で値が全て 0 の配列 a に対して， Q 個の以下のクエリを適用する．
    • クエリ q : l_q \leq i \lt r_q なる各整数 i について， a_i に F_{i-l_q} を加算する．ただし， F_i は i 番目のフィボナッチ数．

この問題を imos 法と同様にして処理することを考えましょう． 重要な性質は，各クエリベクトルにおいて 端である l_q, r_q 付近以外では，フィボナッチ数列の定義より x_{q, i} = x_{q, i-1} + x_{q, i-2} という線形の関係式が成り立つ ことです． このことを考慮すれば， A \boldsymbol{x}_q をスパースにするためには， A として対角成分が 1 ， (i+1, i) 成分及び (i+2, i) 成分が -1 ，それ以外が 0 であるようなものを取れば良さそうです． 例えば N=5 のときは

\begin{align} A = \begin{pmatrix} 1 & 0 & 0 & 0 & 0\\\ -1 & 1 & 0 & 0 & 0\\\ -1 & -1 & 1 & 0 & 0\\\ 0 & -1 & -1 & 1 & 0\\\ 0 & 0 & -1 & -1 & 1 \end{pmatrix}\\\ \end{align}

です．この行列はスパースな下三角行列であり，さらに対角成分が全て非零であることから，必要な性質を全て備えています．

A^{-1} \boldsymbol{y} の計算，すなわち A \boldsymbol{z} = \boldsymbol{y} なる \boldsymbol{z} を求める操作は，

\begin{align} z_1 &= y_1, \\\ - z_1 + z_2 &= y_2, \\\ - z_1 - z_2 + z_3 &= y_3, \\\ - z_2 - z_3 + z_4 &= y_4, \\\ &\vdots \\\ -z_{N-2} -z_{N-1} + z_N &= y_N \\\ \end{align}

より

\begin{align} z_1 &= y_1, \\\ z_2 &= y_2 + z_1, \\\ z_3 &= y_3 + z_1 + z_2, \\\ z_4 &= y_4 + z_2 + z_3, \\\ &\vdots \\\ z_N &= y_N + z_{N-2} + z_{N-1} \\\ \end{align}

となります．累積和とは違う形になっていることが分かると思います．

具体例を見てみましょう． f:id:Theory_and_Me:20200823171257p:plain

線形漸化式で定義される数列

フィボナッチ数列以外でも，なんらかの線形漸化式で定義される数列にもここでの議論が応用できます． まさに冒頭で挙げた問題である Add Recursive Sequence はこれを問うている問題であり，同様の考え方で解くことができます．

注意点としては，線形漸化式の項数が多くなればなるほど，計算量が増えていくということです． K 項間漸化式であれば， A をかけた後のクエリベクトルの非零要素の数は最大 2(K-1) 個となるため，一度の加算に必要な計算量は最大 2(K-1) 回程度となります． また，最後に A^{-1} を掛ける操作にも KN 回程度の計算が必要になります．

まとめ

線形代数を通してみると imos 法の理解が深まり，さらに拡張することができることが分かったと思います． 何かコメントやご意見があればご遠慮なくお願いします． この記事を書くきっかけとなった問題を作り，記事に関してコメントを下さった opt さんに感謝します．

燃やす埋める問題と劣モジュラ関数のグラフ表現可能性 その② グラフ構築編

前回の記事では，競プロ界隈における「燃やす埋める問題」と離散最適化のトピックである「劣モジュラ関数のグラフ表現可能性」の関係性について述べ，与えられた列モジュラ関数が最小カットを通して最小化できるための条件について説明しました．

今回の記事の目的は，実際に問題が与えられたときどのようにグラフを構築すれば良いか，という方法論を説明することにあります． グラフの構築自体は劣モジュラ関数を知らなくても頭をひねればできるのですが，劣モジュラ関数との関係を意識することで以下のようなメリットがあると考えています．

  1. 与えられた問題が最小カットで解けるのか解けないのかの判別がしやすい．
  2. 劣モジュラ関数最小化の形にしてしまえば，機械的にグラフを構築することができる．

個人的に 2 がけっこー嬉しいです． というのも，燃やす埋める問題におけるグラフ構築方法は文献によって方法が様々あり，さらに頭を使って工夫しないといけないものが多いという感覚が個人的にはありました． 慣れた人はうまくやれば良いと思うのですが，慣れていない人は結構混乱するような…．

劣モジュラ関数の最小化の形に落としてしまえば，あまり頭を使わずにグラフを構築する方法論が既に確立されているためこれに乗っかることができる，というのがメリットかもしれないな〜と思っています．

グラフ構築の手順

1. 最小化問題にする

まず，問題が最大化問題になっている場合，コストの符号を反転させるなどして最小化問題にします． 関数値が負になっても特に問題はないので，気にせず符号を反転させてOKです． 最終的に出てくる最適値の符号も反転して出てくることには注意．

2. 1-3変数の劣モジュラ関数の和の形で書く

うまく変数および関数を設定して，与えられた問題を


\begin{align*} \kappa + \sum_i \theta_i (x_i) + \sum_{i< j} \phi_{ij} (x_i, x_j) + \sum_{i< j< k} \psi_{ijk} (x_i, x_j, x_k) \end{align*} \tag{1}


の最小化問題として定式化します． ただし， x_1, \ldots, x_n は \{0, 1\} の値をとる変数であり， \theta_i (x_i), \phi_{ij}(x_i, x_j), \psi_{ijk}(x_i, x_j, x_k) はそれぞれ1変数，2変数，3変数の劣モジュラ関数とします．また， \kappa は定数項です． 定義より，1変数関数は自動的に劣モジュラ関数になることに注意して下さい．

x_1, \ldots, x_n は 「アイテム i を取るなら1, 取らないなら0」のような変数にするとうまくいくことが多いです． 単純な問題なら2変数まであれば十分なことも多いと思います．(「アイテム i  を取ったときに アイテム j を取るとコスト10かかる」などは2変数関数で表せます)

うまく劣モジュラ関数になってくれない場合，ビットを反転させればうまく行く場合があります． x_i を「アイテム i を取るなら0， 取らないなら1」という変数に取り直すイメージです． この辺りは試行錯誤が必要な場所になります（機械的とは何だったのか）．

3. グラフを構築する

さて (1) の最小化問題として定式化できたら，いよいよグラフを構築します．

まず，頂点集合 \{s, t, v_1, \ldots, v_n \} を用意します． s, t は s- t カットを考えるための頂点であり，頂点 v_i は変数 x_i に対応します． この頂点集合に，容量付きの辺及び補助頂点を追加していきます．

辺の引き方，というかコストのかかり方の基本的な考え方は，

  • 容量 C の辺 i \rightarrow j は，頂点 i に値 0 が，頂点 j に値 1 が割り当てられた場合にのみコスト C を発生させる
  • s- t カットなので s には必ず 0 が， t には必ず 1 が割り当てられる
  • 辺の容量は非負でなければならない

の3つです．

重要なこととして，(1) の各項は独立に考えて良いです． つまり，ある項 T のことを考える時は，それ以外の項は完全に無視して T をうまく表現することだけを考えればいいです． 些細なことですが，このことに注意すると思考リソースがかなり節約できる気がします．

ただし，このとき頂点間に多重辺を引いてしまう可能性があります． 多重辺があっても動くような最小カットアルゴリズムの実装なら問題ありませんが，不安な場合や計算時間がギリギリの場合は最小カット問題を解く前に多重辺を解消した方がいいかもしれません．

3-0. 定数項

まず定数項 \kappa ですが，これは最適化と関係ないので無視してOKです．あとで目的関数値が正しくなるよう調整するために， R という変数に加算して記憶することにします: R \leftarrow 0 と初期化しておいて， R \leftarrow R + \kappa．

3-1. 1変数関数

ここから辺を引いていきます．

辺の容量が非負でなければならないという要請から，場合分けが必要です．

\theta_i(0) \leq \theta_i(1) のとき
  • s から v_i に容量 \theta_i(1) - \theta_i(0) の辺を引く．
  • R \leftarrow R + \theta_i(0) とする．

上記のような辺の引き方をすることで， x_i = 0 のときコスト0が， x_i = 1 のときコスト \theta_i(1) - \theta_i(0) がかかるようにできます．これに定数 \theta_i(0) を足してやればもとの \theta_i(x_i)を表せます．

\theta_i(0) > \theta_i(1) のとき
  • v_i から t に容量 \theta_i(0) - \theta_i(1) の辺を引く．
  • R \leftarrow R + \theta_i(1) とする．

1つ目の場合と同様にすると辺の容量が負になってしまうため，少し処理を変える必要があります．考え方は同じ．

f:id:Theory_and_Me:20200316174011p:plain:w540

3-2. 2変数関数

簡単のため，関数値を以下のような表の形式で書くことにします．

f:id:Theory_and_Me:20200316171022p:plain:w400

まず，次の図のように関数を分解します． f:id:Theory_and_Me:20200316165843p:plain このとき，第1項は定数関数，第2項は i のみに依存する1変数関数，第3項は j のみに依存する1変数関数になっているので，3-0, 3-1 で説明した方法で処理できます．

第4項について考えます． これは， v_i から v_j に容量 B+C - A-D の辺を引くことで表現できます．確かに x_i = 0, x_j = 1 の時のみコスト B+C - A-D がかかり，それ以外の時はコストは0になることがわかると思います．

f:id:Theory_and_Me:20200316174516p:plain:w250

ここで， B+C - A-D が非負であることが要請されますが，劣モジュラ性によりこれは必ず成り立ちます．劣モジュラ性はここに効いているんですね．

3-3. 3変数関数

場合分けが必要です． 簡単のため，次の図のように A- H の記号を定めます． f:id:Theory_and_Me:20200316171912p:plain:w400

P := (A+D+F+G)-(B+C+E+H) とおき， P の符号で場合分けします．

(a) P \geq 0 のとき

P_1 = F-B, P_2 = G-E, P_3 = D-C, P_{23}= (B+C)-(A+D), P_{31} = (B+E)-(A+F), P_{12} = (C+E)-(A+G) とおき，関数を以下のように分解します． f:id:Theory_and_Me:20200316170220p:plain

このとき，右辺第1項は定数，第2-4項は1変数関数，第5-7項は2変数関数になっていることがわかるので，3-0, 3-1, 3-2 で説明した方法で処理します． もとの3変数関数の劣モジュラ性より P_{23} \geq 0, P_{31} \geq 0, P_{12} \geq 0 が成り立つことに注意すると，第5-7項の2変数関数は劣モジュラ関数になっていて，ちゃんとグラフ表現できることが保証されます．

第8項について考えます． これは，

  • 補助頂点 u_{ijk} を追加する．
  • v_i から u_{ijk} に容量 P の辺を引く
  • v_j から u_{ijk} に容量 P の辺を引く
  • v_k から u_{ijk} に容量 P の辺を引く
  • u_{ijk} から t に容量 P の辺を引く
  • R \leftarrow R - P

とすることで表現できます．

f:id:Theory_and_Me:20200316211129p:plain:w250

なぜこれで表現できるかを説明します．

グラフ表現可能性の定義より，補助頂点に対する値の割り当ての中でカット値が最小になるものが表現されると考えれば良いです． 例えば， x_i=0, x_j=0, x_k=0 の場合， u_{ijk} に0が割り当てられた場合はカット値は P，1が割り当てられた場合はカット容量は 3 \cdot P となりますが，このうち P が表現されます．

f:id:Theory_and_Me:20200316215056p:plain:w500

このことから， x_i, x_j, x_k に対するそれぞれの割り当てで表現される値は次の図のようになります．

f:id:Theory_and_Me:20200317174526p:plain:w500

このように， x_i=1, x_j=1, x_k=1 の場合にのみ関数値 0 が表現され，それ以外の場合は関数値 P が表現されることになります． あとは全体に定数 -P を足してやれば (これが R \leftarrow R-P に対応する)，所望の関数が表現されるというわけです．

(b) P \lt 0 のとき

P \geq 0 の場合と考え方はほとんど一緒です．

P_1 = C-G, P_2 = B-D, P_3 = E-F, P_{32}= (F+G)-(E+H), P_{13} = (D+G)-(C+H), P_{21} = (D+F)-(B+H) とおき，関数を以下のように分解します． f:id:Theory_and_Me:20200316170250p:plain

このとき，右辺第1項は定数，第2-4項は1変数関数，第5-7項は2変数関数になっていることがわかるので，3-0, 3-1, 3-2 で説明した方法で処理します． もとの3変数関数の劣モジュラ性より P_{23} \geq 0, P_{31} \geq 0, P_{12} \geq 0 が成り立つことに注意すると，第5-7項の2変数関数は劣モジュラ関数になっていて，ちゃんとグラフ表現できることが保証されます．

第8項について考えます． これは，

  • 補助頂点 u_{ijk} を追加する．
  • s から u_{ijk} に容量 -P の辺を引く
  • u_{ijk} から v_iに容量 -P の辺を引く
  • u_{ijk} から v_jに容量 -P の辺を引く
  • u_{ijk} から v_kに容量 -P の辺を引く
  • R \leftarrow R + P

とすることで表現できます． これで表現できる理由は (a) と同様なので，考えてみてください．

f:id:Theory_and_Me:20200316211331p:plain:w250

3-4. 4変数以上でグラフ表現できる関数

4変数以上の関数にはグラフ表現できないものが存在するのですが，全ての4変数以上の関数がグラフ表現できないわけではありません．

特に，以下の2つは容易にグラフ表現できる上に汎用性が高いので，覚えておいて損はないかもしれません．

引数全てが 1 のとき P\ (\lt0)，それ以外のとき 0 をとる関数

すなわち以下のような n 変数関数 \zeta(x_1, \ldots, x_n) のことです:

\begin{align*} \zeta(x_1, \ldots, x_n) = \begin{cases} P \quad (x_1 = x_2 = \ldots = x_n = 1)\\ 0 \quad (\mathrm{otherwise}). \end{cases} \end{align*}


これは，

  • 補助頂点 u を追加する．
  • v_i\ (i=1, \ldots, n) から u に容量 -P の辺を引く
  • u から t に容量 -P の辺を引く
  • R \leftarrow R + P

で表現できます．理由は3変数関数を表現する際に使ったロジックと全く一緒なので，図を書いて考えてみてください．

引数全てが 0 のとき P\ (\lt0)，それ以外のとき 0 をとる関数

すなわち以下のような n 変数関数 \eta(x_1, \ldots, x_n) のことです:

\begin{align*} \eta(x_1, \ldots, x_n) = \begin{cases} P \quad (x_1 = x_2 = \ldots = x_n = 0)\\ 0 \quad (\mathrm{otherwise}). \end{cases} \end{align*}


これは，

  • 補助頂点 u を追加する．
  • u から v_i\ (i=1, \ldots, n) に容量 -P の辺を引く
  • s から u に容量 -P の辺を引く
  • R \leftarrow R + P

で表現できます．これも図を書いてみれば理由はすぐにわかると思います．

4. 最小 s- t カット問題を解いて答えを得る

最後に，構築されたグラフにおいて s- t カットを求めます．使うアルゴリズムは Ford-Fulkerson でも Edmonds-Karp でも Dinic でも Goldberg-Tarjan でも何でもどうぞ．

最小カット容量値が得られたら，ここまで計算しておいた R を足してやることで元の問題の最小値が求まります． 元の問題が最大化問題なら符号を反転することをお忘れなく．

最適値だけでなく最適解も必要な場合は，最小カットにおいて頂点 v_i に0が割り当てられているか1が割り当てられているかを見ることで x_i の値を決めることができます．

例題

MUL (ARC 85)

atcoder.jp

詳しい設定はリンク先を読んで頂くとして， とりあえず最大化問題になっているので符号を入れ替えて最小化問題にしてやって整理すると，

  • 各宝石 i を割るか割らないか選ぶ
  • 宝石 i を割らなければ -a_i 円貰う
  • ただし， j が i で割り切れるとき，「宝石 i を割るけど宝石 j を割らない」は許されない
  • 貰う合計金額を最小化せよ

ということになります．これは， x_i を「宝石 i を割るとき1, 割らないとき0」という変数と考えて，

  • \theta_i (0) = -a_i, \theta_i (1) = 0
  • \phi_{ij} (0, 0) = \phi_{ij} (0, 1) = \phi_{ij} (1, 1) = 0, \phi_{ij} (1, 0) = +\infty

なる関数を用意して，

\begin{align*} \sum_i \theta_i (x_i) + \sum_{i| j} \phi_{ij} (x_i, x_j) \end{align*}


を最小化する問題として捉えられます．（ここまで前の記事と同じ）

さて，上の手順に従えばこの場合のグラフ構築の手順は簡単で，

  • i=1, \ldots, N に対して， -a_i \gt 0 ならば v_i \rightarrow t に容量 -a_i の辺を引く． -a_i \lt 0 ならば s \rightarrow v_i に容量 a_i の辺を引き， R \leftarrow R-a_i とする．
  • i=1, \ldots, N, j=i+1, \ldots, N に対して， j が i で割り切れるならば， j \rightarrow i に容量 \infty の辺を引く．

とすれば OK です．

Petya and Graph (Educational Codeforces Round 55)

codeforces.com

この問題も最大化問題なので符号を反転して最小化問題にして少し考えると

  • グラフ G=(V, E) がある
  • 各頂点を選ぶか選ばないか決める
  • 頂点 i を選ぶと重み a_i\ (a_i>0) を得る
  • 頂点 i と頂点 j を同時に選び， ij 間に辺がある場合，重み -w_{ij}\ (w_{ij}>0) を得る
  • 重みの和を最小化せよ．

という問題になります．これは， x_i を「頂点 i を選ぶとき1, 選ばないとき0」という変数と考えて，

  • \theta_i (0) = 0, \theta_i (1) = a_i
  • \phi_{ij} (0, 0) = \phi_{ij} (0, 1) = \phi_{ij} (1, 0) = 0, \phi_{ij} (1, 1) = -w_{ij}

なる関数を用意して

\begin{align*} \sum_{i \in V} \theta_i (x_i) + \sum_{(i, j) \in E} \phi_{ij} (x_i, x_j) \end{align*}


を最小化する問題として捉えられます．（ここまで前記事と同じ）

さて，上の手順に従うと，以下のようにグラフを構築すれば OK です．

  • i=1, \ldots, n に対して， s \rightarrow v_i に容量 a_i の辺を引く．
  • 入力のグラフの各辺 (i, j) について， v_j \rightarrow t に容量 w_{ij} の辺を引き， R \leftarrow R - w_{ij} とし， v_i \rightarrow v_j に容量 w_{ij} の辺を引く．

上の手順は \phi_{ij} を分解してそれぞれ表現していますが， \phi_{ij} が 3-4 で説明した「全ての引数が1のときに P\ (P \lt 0)，それ以外のとき 0 をとる関数」になっていることに注意すると次のような表現も可能です．

  • i=1, \ldots, n に対して， s \rightarrow v_i に容量 a_i の辺を引く．
  • 入力のグラフの各辺 (i, j) について，補助頂点 u_{ij} を用意し， v_i \rightarrow u, v_j \rightarrow u_{ij}, u_{ij} \rightarrow t にそれぞれ容量 w_{ij} の辺を引き， R \leftarrow R - w_{ij} とする．

ここから分かるように，グラフ表現の方法は一意ではありません．

まとめ

グラフ表現可能な劣モジュラ関数の最小化問題の形にしてしまえば，かなり機械的にグラフを構築できることが分かっていただけたと思います．

色々と場合わけでややこしくなってしまいましたが，要はやっていることは「定数は記憶しておいて後は辻褄を合わせる」「 s \rightarrow v_i もしくは v_i \rightarrow t で`1変数関数を表現する」「 v_i \rightarrow v_j で2変数関数を表現する」「補助頂点をうまく使って3変数以上の関数を表現する（できない場合もある）」の4つで，関数をうまく分解することでこの4つを使える形に持っていっている，というのが直感的な理解だと思います．

もちろん，ここで書いた手順は一つの例に過ぎないので，自分にあった方法でグラフを構築すればいいと思います．皆様，良き燃やす埋めるライフを！

もしかしたら，もう少し発展的な内容を扱ったその③を書くかもしれません．ただ，書くにしても色々調べる必要があるので時間はかかりそうです．

参考文献

  • [1] V. Kolmogorov and R. Zabih. What energy functions can be minimized via graph cuts? IEEE Transaction on Pattern Analysis and Machine Intelligence, 26(2):147–159, 2004.

基本的にこの記事の内容は [1] の内容をまとめたものになっているので，詳しく知りたい方はこちらを読んで頂くと理解が深まると思います．一部の図を [1] からお借りしています．

燃やす埋める問題と劣モジュラ関数のグラフ表現可能性 その①

競プロ界隈でいわゆる「燃やす埋める問題」と呼ばれる問題群があります．（このネーミングが適切かどうかには賛否両論あるようですが，広く用いられているようなので本記事中では用います） それほど出題頻度は高くないようですが，知らないと解くのが難しいタイプの問題なので，前もって勉強しておくことが重要です．

この燃やす埋める問題ですが，競プロの界隈から離れて離散最適化研究の界隈から見ると，実は「劣モジュラ関数のグラフ表現可能性」と呼ばれるトピックと非常に強く関係しています． この「燃やす埋める問題」と「劣モジュラ関数のグラフ表現可能性」との関係を知っていると，

  • 与えられた問題が最小カットを用いて解けるのかどうか判断しやすくなる
  • 最小カットを用いて解ける場合に，グラフの構築が機械的にできるようになる

というメリットがあるような気がします．

燃やす埋める問題を解説している記事はたくさんありますが，劣モジュラ関数の観点から論じているものは殆どないようだったのでこの記事で概観してみました．

燃やす埋める問題と \{0, 1\}^n 上の関数の最小化問題

いわゆる「燃やす埋める問題」とは以下のような問題です．

n 個のアイテムがあるとき，それぞれを「燃やす」か「埋める」か決める．このとき，「燃やす」「埋める」のパターンに応じてお金がかかったり逆にお金が貰えたりする（例えば，「アイテム1を燃やした10円かかる」「アイテム2を燃やしたときにアイテム3を埋めたら20円もらえる」など）．このとき，うまく各アイテムを「燃やす」か「埋める」か決めて，必要なお金を最小化せよ．

「アイテム2を燃やしたときにアイテム3は埋められない」などの「禁止」の制約もあり得ますが，これはお金 +\infty がかかると考えればOKです．また，最大化問題の場合は符号を反転させればOKです．

さて，このような問題は \{0, 1\}^n 上の関数 f: \{0, 1\}^n \to \mathbb{R}\cup\{+\infty\} を最小化する問題と考えることができます． 各アイテムが変数 x_i に対応していて， x_i=0 が「アイテム iを燃やす」ことに， x_i=1 が「アイテム i を埋める」ことに対応します． そして，全体でかかるお金が f(x_1, x_2, \ldots, x_n) で表されていて， x_1, x_2, \ldots, x_n をうまく決めることで f を最小化します．

この最小化問題は， f に何の制限もなければNP-Hardです． これが効率的に解けるはずがないっていうのは直感的にも分かりますよね．

劣モジュラ関数

さて，気になるのは関数のクラスを制限すれば効率的に解くことができるかどうか，ということです． このトピックに関しては様々な研究がなされていますが，特に重要なのがこの記事の主題である劣モジュラ関数です．

劣モジュラ関数とは， \{0, 1\}^n 上の関数 f で，任意の x, y \in \{0, 1\}^n に関して

\begin{align*} f(x)+f(y) \geq f(x \land y) + f(x \lor y) \end{align*} \tag{1}


が成り立つもののことを言います．ただし， x \land y は x と y に関して変数ごとに論理積をとったものを， x \lor y は x と y に関して変数ごとに論理和をとったものを表すこととします．

文献によっては，劣モジュラ関数の定義は集合 V 上の集合関数 f: 2^V \rightarrow \mathbb{R} で，任意の S, T \subseteq 2^V に関して

\begin{align*} f(S)+f(T) \geq f(S \cap T) + f(S \cup T) \end{align*} \tag{2}


が成り立つようなもの，となっていることがあります（というかこっちの方が多い？）． (2)における集合を指示関数に読み替えることで，(1)と(2)は等価であることが容易に確かめられます． 今回は(1)の定義で話を進めていきます．

実は劣モジュラ関数の最小化問題は多項式時間で解くことが可能です．(1)という緩い（?）条件を加えるだけで \{0, 1\}^n 上の関数の最小化が多項式時間でできるというのはけっこー驚きです． また，ここでは詳しく述べませんが，劣モジュラ関数は見方を変えると直感的で自然な解釈が可能で（限界効用逓減性），様々な現実の問題をモデリングすることができます． このように，最適化のしやすさとモデリングにおける有用性を兼ね備えていることから，劣モジュラ関数は様々な分野で重要視されています．

ちなみに，劣モジュラ関数の最大化はNP-Hardですが，効率的な近似アルゴリズムが設計できることが知られており，こちらに関しても様々な結果が知られています．本記事では最大化の話はしませんがこれはこれで面白いトピックです．

グラフ表現可能な劣モジュラ関数

さて，劣モジュラ関数は多項式時間で最小化できると言いましたが，「簡単にできる」とは言っていません． というのも，多項式時間とはいえども n の肩に乗る指数が大きく，アルゴリズムも非常に複雑で実装が難しいからです． これでは現実の問題を解くために用いることは難しそうです…

しかし光明はあります．実は一部の劣モジュラ関数は，「適切なグラフを作りその上で最小カット問題を解くことで最小化することができる」ことが知られています．最小カット問題は比較的シンプルなアルゴリズム (Dinic のアルゴリズムなど) で高速に解くことができるので，めでたしめでたしという訳です．

上記の内容を正確に議論するため，グラフ表現可能な関数という概念を導入します． \{0, 1\}^n 上の関数 f がグラフ表現可能であるとは，ある非負枝容量付き有向グラフ G=(V, E) と定数 \kappa が存在して，

  • V \supseteq \{ s, t, 1, \ldots, n \}

  • 任意の x=(x_1, \ldots, x_n) \in \{ 0, 1\}^n に対して f(x) = \mathrm{min} \{ C(X) \mid X\ は\ s {\rm -} t\ カット, X(i) = x_i\ (i=1, \ldots, n) \} + \kappa

が成り立つことを言います [1]．ただし，ここでいう s- t カットとは，グラフの頂点 v \in V に対する 0-1 割り当て X: V \to \{0, 1\} のうち， X(s)=0, X(t)=1を満たすもののことを言います．また， C(X) は カット X のカット容量を表します．

この定義はすぐには分かりづらいのですが，要は

  • \{s, t, 1, \ldots, n\} にいくつかの補助頂点を加えたものを頂点集合 V として，そこに適当に容量つきの辺を引いてグラフ G = (V, E) を作る
  • x=(x_1, \ldots, x_n) \in \{ 0, 1\}^n が与えられたとき，頂点 i\ (i=1, \ldots, n) の割り当てを x_i に固定した s- t カット集合を考える（追加した補助頂点の割り当ては任意なので，複数の s- t カットが考えられる）． この s- t カット集合の中でカット容量が最小になるものを X^{*} としたとき， C(X^{*}) + \kappa = f(x) となる．これが全ての x \in \{ 0, 1\}^n について成り立つ．

ということです．

少し考えれば，このような性質を満たすグラフ上で最小 s- t カットを求めれば， f の最小化ができることが分かると思います．また，最小カットにおける頂点 1, \ldots, n の割り当てを見ることで，もとの問題の最適解も復元できます．

実は，任意のグラフ表現可能な関数は劣モジュラ関数です．このことはカット関数そのものが必ず劣モジュラ関数になることと，少々の式変形から導くことができます． すなわち，「 \{0, 1\}^n 上の関数」と「劣モジュラ関数」と「グラフ表現可能な関数」は次の図のような関係になっています．

f:id:Theory_and_Me:20200313154438p:plain
関数クラスの関係

ここまで導入した言葉を用いると，競プロにおける「燃やす埋める問題」は，「グラフ表現可能な劣モジュラ関数を最小カットアルゴリズムによって最小化する問題」に概ね一致します．（ビット反転を考慮する必要があるため「概ね」と言っています．詳しくは後で説明します．）

どのような関数がグラフ表現可能なのか？

さて，ここまでくると

  • どのような関数がグラフ表現可能なのか？
  • どのようなグラフを構築すれば表現できるのか？

が気になってきます．これらに関する知見があれば，問題が与えられたときにそれがグラフカットによって解くことが可能かどうかが判別でき，さらに適切なグラフを構築することで最小化を行うことができるからです．

これらの問いへの解答は離散最適化において重要なトピックであり，様々な研究がなされてきました． とりあえずこの記事の中では1つ目の問いについての代表的な結果を示します． 問題を解く上では2つ目の問いも重要なのですが，長くなってしまうのでについては次の記事（その②）に書こうと思います．

1変数関数＋2変数劣モジュラ関数

さて，まずシンプルな例として以下の形で表される関数について考えてみます．

\begin{align*} \sum_i \theta_i (x_i) + \sum_{i< j} \phi_{ij} (x_i, x_j) \end{align*} \tag{3}


ただし， \phi_{ij}(x_i, x_j) は2変数劣モジュラ関数とします（すなわち， \phi_{ij}(0, 1)+ \phi_{ij}(1, 0) \geq \phi_{ij}(0, 0) + \phi_{ij}(1, 1) が成立）． 簡単な計算より，1変数関数と劣モジュラ関数，及び劣モジュラ関数と劣モジュラ関数の和はまた劣モジュラ関数になるので，上記の形で表される関数は劣モジュラ関数になります．

この劣モジュラ関数はグラフ表現可能でしょうか？答えはYESです．1変数関数と2変数劣モジュラ関数の和の形で表される任意の関数は，グラフ表現可能であることが知られています [2]．

具体的なグラフの構築方法はその②で説明しますが， 頂点集合 V=\{s, t, 1, \ldots, n\} を用意して，

  • 1変数関数1つにつき辺を高々1本
  • 2変数関数1つにつき辺を高々3本

加えればグラフを構築できます．そのため，構築されるグラフの頂点数，辺数も n の多項式で抑えられ，最小カットにより効率的に最小化できます．

例題

MUL (ARC 85)

atcoder.jp

詳しい設定はリンク先を読んで頂くとして， とりあえず最大化問題になっているので符号を入れ替えて最小化問題にしてやって整理すると，

  • 各宝石 i を割るか割らないか選ぶ
  • 宝石 i を割らなければ -a_i 円貰う
  • ただし， j が i で割り切れるとき，「宝石 i を割るけど宝石 j を割らない」は許されない
  • 貰う合計金額を最小化せよ

ということになります．これは， x_i を「宝石 i を割るとき1, 割らないとき0」という変数と考えて，

  • \theta_i (0) = -a_i, \theta_i (1) = 0
  • \phi_{ij} (0, 0) = \phi_{ij} (0, 1) = \phi_{ij} (1, 1) = 0, \phi_{ij} (1, 0) = +\infty

なる関数を用意して，

\begin{align*} \sum_i \theta_i (x_i) + \sum_{i| j} \phi_{ij} (x_i, x_j) \end{align*}


を最小化する問題として捉えられます．

さて，簡単な計算により \phi_{ij} は劣モジュラ関数であることがわかるので，この関数はグラフ表現可能であり，最小カットを用いて最小化できることが分かります．

Petya and Graph (Educational Codeforces Round 55)

codeforces.com

この問題も最大化問題なので符号を反転して最小化問題にして少し考えると

  • グラフ G=(V, E) がある
  • 各頂点を選ぶか選ばないか決める
  • 頂点 i を選ぶと重み a_i を得る
  • 頂点 i と頂点 j を同時に選び， ij 間に辺がある場合，重み -w_{ij}\ (w_{ij}>0) を得る
  • 重みの和を最小化せよ．

という問題になります．これは， x_i を「頂点 i を選ぶとき1, 選ばないとき0」という変数と考えて，

  • \theta_i (0) = 0, \theta_i (1) = a_i
  • \phi_{ij} (0, 0) = \phi_{ij} (0, 1) = \phi_{ij} (1, 0) = 0, \phi_{ij} (1, 1) = -w_{ij}

なる関数を用意して

\begin{align*} \sum_{i \in V} \theta_i (x_i) + \sum_{(i, j) \in E} \phi_{ij} (x_i, x_j) \end{align*}


を最小化する問題として捉えられます．

w_{ij}>0 より \phi_{ij} は劣モジュラ関数であることがわかるので，この関数はグラフ表現可能であり，最小カットを用いて最小化できることが分かります．

1変数関数＋2変数劣モジュラ関数+3変数劣モジュラ関数

さて，それではもう少し広い関数のクラスとして，以下の形で表される関数はどうでしょうか？


\begin{align*} \sum_i \theta_i (x_i) + \sum_{i< j} \phi_{ij} (x_i, x_j) + \sum_{i< j< k} \psi_{ijk} (x_i, x_j, x_k) \end{align*} \tag{4}


ただし， \psi_{ijk}(x_i, x_j, x_k) は3変数劣モジュラ関数とします．

この劣モジュラ関数はグラフ表現可能でしょうか？ なんとこの答えもYESです．1変数関数と2変数劣モジュラ関数と3変数劣モジュラ関数の和の形で表される任意の関数も，グラフ表現可能であることが知られています [3]．

具体的なグラフの構築方法はその②で説明しますが， 頂点集合 V=\{s, t, 1, \ldots, n\} を用意して，

  • 1変数関数1つにつき辺を高々1本
  • 2変数関数1つにつき辺を高々3本
  • 3変数関数1つにつき補助頂点を高々1つ，辺を高々16本

加えればグラフを構築できます．そのため，構築されるグラフの頂点数，辺数も n の多項式で抑えられ，最小カットにより効率的に最小化できます．辺だけではなく補助頂点を加える必要があるのが2変数関数と違うところですね．

4変数以上の劣モジュラ関数

さて，ここまできたら次に気になるのは4変数劣モジュラ関数が入ってきてもグラフ表現できるのか！？になりますが，良いニュースはここでおしまいです．

実は，4変数以上の劣モジュラ関数の中には，いくら頂点や辺を付け加えたとしても絶対にグラフ表現できないものが存在することが，2009年に Živný らによって示されています [4]． まだ僕はこの証明はあまり理解できていません．悲しいね． 詳しい人曰く，「グラフ表現可能ならこういう不等式を満たさないといけないけど，この4変数関数は満たしてないから，グラフ表現不可能」という論法で，そこまで難しくは無いとのことです．

ビット反転

さて，こんな感じで関数がグラフ表現できる条件を挙げてきましたが，ちょっと厄介な存在が残っています． それは，「劣モジュラ関数ではないけれど，適切にビット反転すると劣モジュラ関数になるような関数の存在」です．

例えば， \phi_{ij}(0, 0) = 1, \phi_{ij}(1, 0) = 0, \phi_{ij}(0, 1) = 0, \phi_{ij}(1, 1) = 2 なる2変数関数 \phi_{ij}(x_1, x_2) は劣モジュラ関数ではありません． しかし，ここで新しく \phi'_{ij}(x_1, x_2) = \phi_{ij}( \lnot x_1, x_2) という， x_2 を反転させた関数 \phi'_{ij}(x_1, x_2) を考えてみます． すると， \phi’_{ij}(0, 0) = 0, \phi’_{ij}(1, 0) = 1, \phi’_{ij}(0, 1) = 2, \phi’_{ij}(1, 1) = 0 となるため， \phi'_{ij}(x_1, x_2) は劣モジュラ関数になります．

そして，「適切なビット反転をすることでグラフ表現可能な劣モジュラ関数になるような関数」もまた，最小カットで最小化可能です． この場合，含まれる全ての項に関して同時にビット反転をする必要があることに注意してください． 例えば \phi_{12}(x_1, x_2) + \phi_{23}(x_2, x_3) のような形の関数において x_2 を反転させる場合， \phi_{12}(x_1, \lnot x_2) でだけなく \phi_{23}( \lnot x_2, x_3) も劣モジュラ関数になる必要がある，といった感じです．

「適当なビット反転によってグラフ表現可能な劣モジュラ関数にできるかどうか」を効率的に判定するのは難しそうです． そもそも与えられた劣モジュラ関数がグラフ表現可能かを判定する効率的な方法がわかっていないとのこと． そのため，競プロの問題として出てきたら試行錯誤して良い反転を見つける必要がありそうです． 依存関係が二部グラフになっていたりすると，ビット反転しやすかったりするようです．

まとめ

  • 競プロでいう「燃やす埋める問題」は「グラフ表現可能な劣モジュラ関数を最小カットによって最小化する問題」だよ
  • 1-3変数劣モジュラ関数の和の形で表される劣モジュラ関数はグラフ表現可能だよ
  • 4変数が入ってくると無理な場合があるよ
  • ビット反転も考慮する必要があるよ

具体的なグラフの構築方法についてはその②で説明する予定です．

グラフ表現可能性について色々教えてくれた，ゆにさん(@yuni_jp)に感謝！

参考文献

  • [1] V. Kolmogorov and R. Zabih. What energy functions can be minimized via graph cuts? IEEE Transaction on Pattern Analysis and Machine Intelligence, 26(2):147–159, 2004.
  • [2] P. L. Ivănescu. Some network flow problems solved with pseudo-boolean programming. Operations Research, 13(3):388–399, 1965
  • [3] A. Billionnet and M. Minoux. Maximizing a supermodular pseudoboolean function: a polynomial algorithm for supermodular cubic functions. Discrete Applied Mathematics, 12:1–11, 1985
  • [4] S. Živný, D. A. Cohen and P. G. Jeavons. The Expressive Power of Binary Submodular Functions. Discrete Applied Mathematics, 157(15):3347–3358, 2009

ちなみに [1] の論文は画像系のトップジャーナルの論文です．なぜこの話題が画像系のジャーナルに載っているかというと「マルコフ確率場 (MRF) のMAP推定問題」という，画像の復元•ノイズ除去をする際に現れる問題が，実はいわゆる燃やす埋める問題になることが知られているからです．競プロは現実問題の役に立つ！（？）

最小費用流問題を一般化して双対問題を綺麗に書きたい

最近ネットワークフローにハマっている（？）ので，勉強したことを書きます． 一応競プロに役に立つ可能性がなくはないです． あと，簡単のために詳細な数学的議論を省略しているところがあります．

TL;DR

最小費用流問題は一般化すると双対関係が綺麗に書けるよ

最小費用流問題と双対問題

最小費用流問題とは，有効グラフ G=(V, E)，辺 (i, j) \in E のコスト c_{ij}，辺 i \in V の容量 u_{ij}，頂点 i \in V の需要供給 b_{i} が与えられたときに，需要供給を満たしつつ容量制約を満たすフローのうち，コストを最小化するものを求める問題です．数式で書くと以下のように書けます．

\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R}^{|E|}}.& && \sum_{(i, j) \in E} c_{ij} x_{ij} \\ \mathrm{s.t.}& && \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} x_{ji} = b_i \quad (\forall i \in V), \\ &&& 0 \leq x_{ij} \leq u_{ij} \quad (\forall (i, j) \in E) \\ \end{aligned} \end{align*} \tag{1}


1つめの制約がフローが需要供給の制約を満たすことを，2つめの制約がフローが容量制約を満たすことを表現しています．

さて，この最小費用流問題は線形計画問題 (LP) の一種なので，LPとしての双対を考えることで以下の双対問題を考えることができます．

\begin{align*} \begin{aligned} \min_{\boldsymbol{p} \in \mathbb{R}^{|V|}}. && \sum_{(i, j) \in E} u_{ij} \cdot \max(0, p_j - p_i - c_{ij}) + \sum_{i \in V} b_i p_i \\ \end{aligned} \end{align*} \tag{2}


LP の強双対定理から，適切な条件下で主問題と双対問題の最適値は一致します． この性質を利用することで，例えばある問題が双対側の最適化問題として定式化することができるならば，双対をとって主問題に対するアルゴリズムを適用してあげることで最適値を得ることができたりするわけです． （競プロにおける双対の使い方に関しては例えば https://www.slideshare.net/wata_orz/ss-91375739 が詳しいです）

さて，最小費用流問題の双対問題，パッと見ただけでは正直なところ何をしているのかよく分からなくて覚えにくい最適化問題です． これは，最大流問題の双対問題が「頂点集合を二つに分割して分割間の辺の重みを最小化する」（つまり最小カット問題）という分かりやすい解釈を持つことと対照的です．

この記事の目的は，この分かりにくい最小費用流問題の双対問題を覚えやすい綺麗な形で書こうと頑張ることです．

最小凸費用流問題への一般化

ここで突然ですが，最小費用流問題を一般化し，以下のような問題を考えます．

\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R}^{|E|}}.& && \sum_{(i, j) \in E} \phi_{ij}(x_{ij}) \\ \mathrm{s.t.}& && \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} x_{ji} = b_i \quad (\forall i \in V). \\ \end{aligned} \end{align*} \tag{3}


ただし， \phi_{ij}: \mathbb{R} \to \mathbb{R} \cup \{ \pm \infty \} は凸関数とします． ここでの凸関数の定義は， \phi_{ij}(x) \neq \pm \infty, \phi_{ij}(y) \neq \pm \infty なる x, y \in \mathbb{R} 及び 0 \leq t \leq 1 なる t について t \cdot \phi_{ij}(x)+ (1-t) \cdot \phi_{ij}(y) \geq \phi_{ij}(t \cdot x + (1-t) \cdot y) が 成立することと定義します（よくある普通の凸関数の定義を一般化したものになっています）． \pm \infty に関する演算は直感的なものを採用して下さい．

この問題がもとの最小費用流問題 (1) の一般化になっていることは，

\phi_{ij} (x_{ij}) = \left\{ \begin{array}{} c_{ij} x_{ij} & (0 \leq x_{ij} \leq u_{ij})\\ + \infty & (\mathrm{otherwise}) \end{array} \right. \tag{4}


とするともとの問題 (1) に一致することから分かります． 容量制約を破ると無限大の費用がかかるようにすることで，強制的に容量制約を守らせるようにしているわけです． \phi_{ij} が凸関数であることは容易に確かめられます．

最小凸費用流問題の Fenchel 双対

さて，目的関数が非線型になり，問題が LP ではなくなってしまったため，LP の双対定理は適用する事ができません． しかし，Fenchel 双対という概念を用いることで，このような問題にも双対問題を考えることができます． Fenchel 双対は凸最適化問題に適用できる双対で，適当な仮定のもとで強双対定理なども成立します． また，LPの双対は Fenchel 双対の特殊ケースとして導出することができます． Fenchel 双対については詳しくは http://www.misojiro.t.u-tokyo.ac.jp/~murota/lect-surikeikakuhou/fenchel031129.pdf が分かりやすいです．

(3)の Fenchel 双対をとると以下のような最適化問題になります:

\begin{align*} \begin{aligned} \max_{\boldsymbol{p} \in \mathbb{R}^{|V|}}.& && -\sum_{(i, j) \in E} \psi_{ij}(p_j - p_i) - \sum_{i \in V} b_i p_i . \end{aligned} \end{align*} \tag{5}


あるいは最小化問題としてしまった方が綺麗かもしれません（目的関数値の符号が逆転することに注意）．

\begin{align*} \begin{aligned} \min_{\boldsymbol{p} \in \mathbb{R}^{|V|}}.& && \sum_{(i, j) \in E} \psi_{ij}(p_j - p_i) + \sum_{i \in V} b_i p_i . \end{aligned} \end{align*} \tag{6}


ただし， \psi_{ij} は \phi_{ij} の Legendre 変換です:

\psi_{ij}(p) := \sup_{x \in \mathbb{R}} \{ p \cdot x - \phi_{ij}(x) \}. \tag{7}


何やらややこしかったもとの双対問題 (2) に比べて，(6) はかなりすっきりとした表式になっていると思います！

主問題 (3) と双対問題 (6) の関係は，もとの最小費用流問題 (1) と双対問題 (2) の関係の一般化になっています． そのことを確認するために， \phi_{ij} が式 (4) で表される場合の双対問題を考えてみましょう． Legendre 変換の定義式 (7) より，

\begin{align*} \psi_{ij} (p) &= \sup _{x \in \mathbb{R}} \{ p \cdot x - \phi_{ij}(x)\} \\ &= \sup_{0 \leq x \leq u_{ij}} \{ p \cdot x - c_{ij} \cdot x\} \\ &= \sup_{0 \leq x \leq u_{ij}} \{ (p - c_{ij}) \cdot x\} \\ &=\left\{ \begin{array}{} u_{ij} \cdot (p-c_{ij}) & (p > c_{ij})\\ 0 & (p \leq c_{ij}) \end{array} \right. \\ &= u_{ij} \cdot \max(0, p-c_{ij}) \end{align*} \tag{8}


なので， 双対問題 (6) の \psi_{ij} を (8) の式で置き換えてやれば，もとの問題の双対問題 (2) が出てきますね！

制約が変わった場合

主問題 (3) + 双対問題 (6) の形で理解しておくことのメリットとして，主問題の制約が多少変わっても双対問題が簡単に導ける点があります．

例えば，もとの最小費用流問題におけるフローの上限制約がなくなった

\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R}^{|E|}}.& && \sum_{(i, j) \in E} c_{ij} x_{ij} \\ \mathrm{s.t.}& && \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} x_{ji} = b_i \quad (\forall i \in V), \\ &&& x_{ij} \geq 0 \quad (\forall (i, j) \in E) \\ \end{aligned} \end{align*} \tag{9}


を考えてみます．このとき

\phi_{ij} (x_{ij}) = \left\{ \begin{array}{} c_{ij} x_{ij} & (x_{ij} \geq 0)\\ + \infty & (\mathrm{otherwise}) \end{array} \right. \tag{10}


として \phi_{ij}(x) を Legendre 変換すると，

\begin{align*} \psi_{ij} (p) &=\left\{ \begin{array}{} + \infty & (p > c_{ij})\\ 0 & (p \leq c_{ij}) \end{array} \right. \\ \end{align*} \tag{11}


となり，(6) と組み合わせることで双対問題を

\begin{align*} \begin{aligned} \min_{\boldsymbol{p} \in \mathbb{R}^{|V|}}.& && \sum_{i \in V} b_i p_i \\ \mathrm{s.t.}& && p_j - p_i \leq c_{ij} \quad (\forall (i, j) \in E) \\ \end{aligned} \end{align*} \tag{12}


と導くことができます． p_j - p_i > c_{ij} の場合は目的関数が無限大になってしまい解になり得ないので，制約として p_j - p_i \leq c_{ij} が入ってくる点がポイントです．

これ以外にも，制約が l_{ij} \leq x_{ij} \leq u_{ij} とかになっても簡単に双対問題を求めることができます．

その他の最小費用流問題

(6) の形で双対問題が綺麗に書けたのでこの記事の目的は達せられたのですが，もう少し書きます．

\phi_{ij} は凸関数なら何でもいいので，適当に凸関数を持ってくればそれに応じて最小費用流問題と双対問題ができます． 凸関数をカスタマイズして自分だけの最強の最小費用流問題とその双対問題を作ろう！

例えば \phi_{ij}(x) = \frac{1}{2} R_{ij} x^2（ R_{ij} は適当な正実数）としてみると，Legendre 変換は \psi_{ij}(p) = \frac{1}{2R_{ij}}p^2 となり，主問題と双対問題は以下のようになります:

\begin{align*} \begin{aligned} \min_{\boldsymbol{x} \in \mathbb{R}^{|E|}}.& && \sum_{(i, j) \in E} \frac{1}{2} R_{ij} x_{ij}^2 \\ \mathrm{s.t.}& && \sum_{j: (i, j) \in E} x_{ij} - \sum_{j: (j, i) \in E} x_{ji} = b_i \quad (\forall i \in V). \\ \end{aligned} \end{align*} \tag{13}


\begin{align*} \begin{aligned} \min_{\boldsymbol{p} \in \mathbb{R}^{|V|}}.& && \sum_{(i, j) \in E} \frac{1}{2R_{ij}}(p_j - p_i)^2 + \sum_{i \in V} b_i p_i . \end{aligned} \end{align*} \tag{14}


この問題，なんとなく電気回路における電流と電位の関係を表現しているように解釈できそうです． 各頂点 i に電流 b_i が流れ込んでいて，頂点 i と頂点 j の間に抵抗値 R_{ij} の抵抗があるという電気回路を考えます． このとき，主問題 (13) は「回路全体の抵抗での発熱を最小化するような電流を求めよ」という問題になっています． これは，「最小発熱の原理」（電気回路における変分原理で，回路全体での発熱が最小の状態が現実に起こるというもの）から，実際に流れる電流を求める問題になっています． 双対問題 (14) もそんな感じの解釈ができそうで，強双対定理は「電流（ =\boldsymbol{x}）で考えても電位（ =\boldsymbol{p}）で考えても実現する状態は一緒だよ」的なことを言ってそうな感じがします．

よく分からないので電気回路のことを思い出しつつちょっと考えてみます（誰か知ってたら教えて下さい）．

なんとなく思うこと

(3) と (6) の双対関係を見ていると，「フロー」（各頂点で流量の保存則が成り立つもの）と「ポテンシャル」（各辺について，両端の頂点に割り当てられている値の差が重要なもの）には本質的な双対関係があるということが感じられます．

最大流・最小カットの双対もそういう視点で見ることができます． なぜなら，最小カットは「各頂点に 0 か 1 の値を割り当てて，両端の値が異なる辺の重みの和を最小化する」問題として捉えることができて，各頂点に割り振る値がまさにポテンシャルであると解釈できるからです． 最大流問題は最小費用流問題の特殊ケースとして定式化できるので，お時間がある方は実際に適当な \phi_{ij} を設定して双対を取ってみると，気持ちが理解できると思います．

ここまで抽象化すると，なんとなく"世界の原理"みたいなものが垣間見えた感じがしてワクワクしますね！（厨二病）

参考文献

この辺の話は別に僕が考えたわけではなくて，昔から凸解析の分野で研究されていることです．以下の文献を見ればより詳しいことがわかると思います．

  • R. T. Rockafellar (1984), Network Flows and Monotropic Optimization, Wiley-Interscience.
  • 室田一雄 (2013)，離散凸解析と最適化アルゴリズム, 朝倉書店．